Generar cadenas
Vamos a generar cadenas alfanuméricas de una determinada longitud y siguiendo ciertos patrones. Estas cadenas se podrán usar como contraseñas para el maltrecho parque robótico, atacado con facilidad por llevar contraseñas vulnerables, contraseñas de fábrica o fácilmente crackeables por fuerza bruta.
Longitud y combinaciones
Antes de proceder, analicemos como una contraseña - en realidad una simple cadena de texto de longitud limitada - puede convertirse en una buena protección contra un ataque de fuerza bruta si introduce suficiente variedad.
Este tipo de ataques consiste en intentar adivinar la contraseña probando una y otra vez distintas combinaciones, a menudo usando diccionarios o patrones conocidos.
Para empezar, imaginemos algo que en realidad no existe -o al menos no debería existir- como password: una sola cifra decimal de 0 a 9 como contraseña. Si adivinas el número pasas.
Como es lógico, adivinar la password en este caso se puede conseguir en un rango de 1 a 10 intentos. No es nada seguro.
Ahora imaginemos una contraseña formada por un PIN de 4 dígitos. ¿Cuántas combinaciones posibles hay?
10 x 10 x 10 x 10 = 10.000
Ya es algo mejor, pero sigue siendo insuficiente si automatizamos el proceso para probar combinaciones.
¿Qué sucede si vamos más allá?
Si usamos 6 posiciones y solo números:
10⁶ = 1000.000
Si combinamos letras mayúsculas, dígitos y al menos un carácter especial:
- 26 letras mayúsculas
- 10 dígitos
- 10 caracteres especiales (por ejemplo: !@$%#*_-^| )
Suman 46 glifos posibles en cada posición:
46⁸ = 2 * 10¹³ combinaciones posibles
Si las cadenas son generadas al azar, evitando coincidencias con palabras reales, el tiempo empleado en adivinar una contraseña por fuerza bruta puede ir de imposible a varios años, dependiendo de los recursos del atacante. Y estamos hablando de una sola contraseña.
La vulnerabilidad
Son miles de robots…
La IA de la terminal ancestral decía que los robots fueron el vector de entrada del virus al sistema - a través de su interfaz de proximidad. La vulnerabilidad consiste en que todos los robots comparten de fábrica el mismo PIN de acceso: 123456 y también una clave interna de 128 bits con la que se cifran las comunicaciones. El virus fue implantado conociendo de antemano ambos datos.
Cada vez que el sistema primigenio intenta restaurarse los robots contagiados vuelven a transmitir el virus.
La solución pasa por generar para cada robot una clave distinta de 128 bits (16 bytes) y un PIN nuevo. Las claves nuevas no se repetirían ni seguirán un patrón secuencial - Eso significa que, incluso si un atacante logra adivinar una contraseña, le quedan todas las demás por adivinar. Incluso si lo hacen en paralelo, buena suerte con su superalgoritmo de fuerza bruta porque estaría echando humo durante mucho, mucho tiempo.
La IA de la terminal antigua es capaz de transmitir la orden de sobreescritura de claves y pins, pero no puede generarlos a la velocidad suficiente.
En cuanto las claves y los nuevos PIN estén implantados en los robots - quedarán incomunicados temporalmente, el sistema global podrá intentar restaurarse desde una copia de seguridad.
El virus vive en el tiempo de ejecución.
Las claves que son aleatorias deben generarse en tiempo de ejecución, ya que no son deterministas.
Generar PINs
Los PIN nuevos los podemos preparar en tiempo de compilación, porque al ser números en un rango limitado (en 6 dígitos cabe desde 000000 a 999.999) podemos hacer una selección determinista.
Aunque sean deterministas los PINs no deben de ser fácilmente deducibles así que vamos a hacer una fórmula simple pero no obvia.
pins.zig |
|
const std = @import("std"); const print = std.debug.print; // obtener el pin para un índice fn get_pin4index(n_x: usize) usize { const n_a = n_x + 1; // formula de números pentagonales limitada a 6 cifras return (n_a * (3 * n_a - 1)) / 2 % 1_000_000; } pub fn main() void { // variable definida en tiempo de compilación comptime var a_pins: [1000]usize = undefined; // bloque ejecutado por el compilador comptime { @setEvalBranchQuota(2000); for (0..a_pins.len) |n_i| { a_pins[n_i] = get_pin4index(n_i); } } // bucle ejecutado en tiempo de ejecución para imprimir // los pins generados en tiempo de compilación for (a_pins[0..10].*, 0..) |n_pin, n_i| { print("a_pins[{}]: {}\n", .{ n_i, n_pin }); } } |
|
$ zig run pins.zig |
|
a_pins[0]: 1 a_pins[1]: 5 a_pins[2]: 12 a_pins[3]: 22 a_pins[4]: 35 a_pins[5]: 51 a_pins[6]: 70 a_pins[7]: 92 a_pins[8]: 117 a_pins[9]: 145 |
Obtenemos 1000 códigos PIN usando una fórmula matemática para generar una serie numérica. Es la fórmula de los números pentagonales.
El enésimo número pentagonal se calcula así:
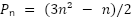
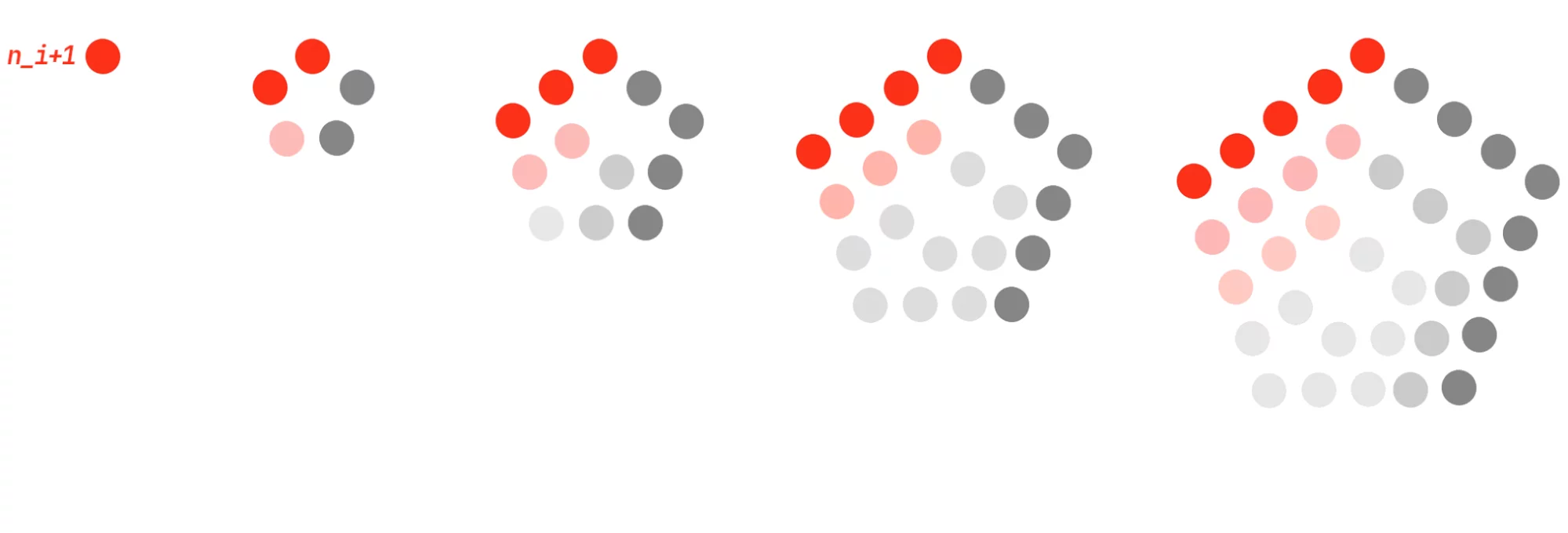
Los números generados así siguen la secuencia: 1, 5, 12, 22, 35 …
Progresión de números pentagonales |
|
|
|
n_i |
0 |
1 |
2 |
3 |
4 |
|
a_pins[n_i] |
1 |
5 |
12 |
22 |
35 |
Cada número muestra cómo crece el patrón al añadir capas al pentágono. Son como los números triangulares o cuadrados, pero con cinco lados. Esta serie suele aparecer en teorías combinatorias.
Usamos la palabra clave comptime para definir variables de tiempo de compilación y bloques enteros que serán ejecutados en tiempo de compilación.
|
// variable definida en tiempo de compilación comptime var a_pins: [1000]usize = undefined; // bloque ejecutado por el compilador comptime { @setEvalBranchQuota(2000); for (0..a_pins.len) |n_i| { a_pins[n_i] = get_pin4index(n_i); } } |
No cualquier bloque de instrucciones puede ser ejecutado por el compilador. En cuanto tenemos eventos input output, contenido desconocido en tiempo de compilación etc - el bloque deja de ser válido para comptime. A veces puede resultar un reto ajustar las cosas para que el código quede totalmente independiente del tiempo de ejecución. En este caso - los verdaderos números aleatorios no son posibles de generar en tiempo de compilación, pero usamos un truco para que parezca que no siguen una progresión matemática.
setEvalBranchQuota
El compilador tiene límites establecidos para evitar que las evaluaciones en comptime se alarguen demasiado. Por eso estamos usando la instrucción:
|
@setEvalBranchQuota(2000); |
Así aumentamos el límite evaluación en tiempo de compilación. Sin esta instrucción el compilador nos da un error:
|
pins.zig:17:40: error: evaluation exceeded 1000 backwards branches a_pins[n_i] = get_pin4index(n_i); ~~~~~~~~~~~~~^~~~~ |
El error nos comunica que la evaluación en tiempo de compilación está superando el límite predeterminado de iteraciones hacia atrás (backward branches). Esto es una medida de protección del compilador contra bucles infinitos o evaluaciones excesivas, y en nuestro caso ha detectado muchas iteraciones por lo que decide abortar la misión. Aumentamos el número a 2.000 porque sabemos que la fórmula que usamos es segura y por lo que podemos ver a simple vista necesitamos 1000 iteraciones completas para generar los PINs. No solo nuestras iteraciones visibles cuentan - también las ramas internas (branches) de ejecución: llamadas a funciones, evaluaciones de condiciones, comprobaciones de seguridad, etc. 2000 puede parecer una cantidad elevada para el compilador pero es manejable mientras sepamos lo que hacemos y se lo indiquemos expresamente.
Si no estás seguro del valor exacto que necesitas para @setEvalBranchQuota, puedes ir con un valor conservador puesto un poco a ojo con el doble de tus iteraciones visibles y vas aumentándolo si es necesario. El compilador te pondrá la queja si te equivocas.
Podrías pensar: ¿por qué no poner siempre un valor muy alto y olvidarnos del problema? El “peligro” de poner un valor excesivamente alto no es que tu programa vaya a funcionar peor, de hecho, una vez compilado, este número no influye para nada en el rendimiento. Pero hacer las cosas así no es una buena práctica: podría ocultar bucles casi-infinitos accidentales, alargar el tiempo de compilación innecesariamente y hacer tu código menos mantenible. Además, no hay como saber lo que se hace para crear cosas que funcionen bien.
Pins como cadenas
Para poder usar los números generados como PINs, necesitamos que tengan 6 dígitos. Para ello, hay que enviarlos como cadenas de texto, ya que, por ejemplo, 1 debe ser enviado como 000001. También hay que tener en cuenta que las cadenas como 000001, 000002 etc van a ser fácilmente deducidas en un ataque automatizado así que vamos a empezar desde un índice más alto, definido en la constante N_START.
Por lo tanto procedemos a transformarlos en cadenas:
pins_strings.zig |
|
const std = @import("std"); const print = std.debug.print; // obtener un pin para un índice fn get_pin4index(n_x: usize) usize { const n_a = n_x + 1; // formula de números pentagonales return (n_a * (3 * n_a - 1)) / 2 % 1_000_000; } // convertir el número a una cadena rellena con ceros a la izquierda fn left_pad_zeros(n_a: usize, n_len: usize) [n_len]u8 { comptime var s_resp: [n_len]u8 = undefined; for (0..n_len) |n_ix| { s_resp[n_ix] = '0'; } var n_x: usize = n_a; if (n_x == 0) return s_resp; for (0..s_resp.len - 1) |n_i| { const n_pos = s_resp.len - 1 - n_i; const n_digit = n_x % 10; s_resp[n_pos] = @as(u8, '0' + n_digit); n_x = n_x / 10; } return s_resp; } // declaramos la longitud del PIN máxima del PIN const N_PIN_LENGTH = 6; // iniciamos la serie en números un poco más altos const N_START = 100; pub fn main() void { comptime var a_pins: [1000][N_PIN_LENGTH]u8 = undefined; comptime { // en tiempo de compilación: // mínimo tenemos 1000 * (6 + 6) = 12000 iteraciones visibles // 1000 del bucle for y (6 + 6) de left_pad_zeros // sumado a las ~2000 del ejemplo anterior = 14000 @setEvalBranchQuota(14000); for (0..a_pins.len) |n_i| { // obtenemos el pin en función del indice const n_pin = get_pin4index(n_i + N_START); // convertirmos el pin a cadena rellena con ceros por la izquierda a_pins[n_i] = left_pad_zeros(n_pin, N_PIN_LENGTH); } } // imprimimos los primeros 5 y los últimos 5 // PIN para comprobar el resultado for (a_pins[0..5].*, 0..) |s_pin, n_i| { print("a_pins[{}]: {s}\n", .{ n_i, s_pin }); } print("...\n", .{}); const n_last = a_pins.len; for (a_pins[n_last - 5 .. n_last].*, n_last - 5..) |s_pin, n_i| { print("a_pins[{}]: {s}\n", .{ n_i, s_pin }); } } |
|
$ zig run pins_strings.zig |
|
a_pins[0]: 015251 a_pins[1]: 015555 a_pins[2]: 015862 a_pins[3]: 016172 a_pins[4]: 016485 ... a_pins[995]: 001276 a_pins[996]: 004565 a_pins[997]: 007857 a_pins[998]: 011152 a_pins[999]: 014450 |
Este sí es el formato correcto de un PIN.
Quien inventó el dicho castellano de alguien o algo es un cero a la izquierda (es decir - que no cuenta para nadie), no sabía que algún día las contraseñas y los PINs iban a tener en cuenta el valor de esos ceros. Al menos su valor ASCII, el 48 para ser exactos.
Si te fijas verás como los últimos PINs vuelven a valores más bajos. El módulo “% 1000_000” hace que los números “den la vuelta” cuando pasan por encima de los 6 dígitos y vuelven a los valores bajos. Es decir, nos quedamos con la parte de las últimas 6 cifras sea cual sea el número. Esto también hace que los PINs sean menos predecibles.
Permutación simple
Ahora, como último paso de generación de nuestra serie de “PINs imprevisibles”, vamos a mezclarlos un poco - pero como esto sucede en tiempo de compilación - también será una mezcla determinista. De esta forma, aunque la serie haya sido generada mediante varios pasos deterministas, no es tan fácil deducir cuáles fueron esos pasos mirando el resultado final.
pins_permuted.zig |
|
const std = @import("std"); const print = std.debug.print; // obtener un pin para un índice fn get_pin4index(n_x: usize) usize { const n_a = n_x + 1; // formula de números pentagonales return (n_a * (3 * n_a - 1)) / 2 % 1_000_000; } // convertir el número a una cadena rellena con ceros a la izquierda fn left_pad_zeros(n_a: usize, n_len: usize) [n_len]u8 { comptime var s_resp: [n_len]u8 = undefined; for (0..n_len) |n_ix| { s_resp[n_ix] = '0'; } var n_x: usize = n_a; if (n_x == 0) return s_resp; for (0..s_resp.len - 1) |n_i| { const n_pos = s_resp.len - 1 - n_i; const n_digit = n_x % 10; s_resp[n_pos] = @as(u8, '0' + n_digit); n_x = n_x / 10; } return s_resp; } fn get_permuted_index(n_i: usize, n_items: usize) usize { // Semilla simple determinista return (n_i * 524287) % n_items; } // declaramos la longitud del PIN máxima del PIN const N_PIN_LENGTH = 6; const N_START = 100; // declaramos el total de PINs creados const N_TOTAL_PINS = 1000; pub fn main() void { comptime var a_pins: [N_TOTAL_PINS][N_PIN_LENGTH]u8 = undefined; comptime { // añadimos 1000 más por la llamada a get_permuted_index @setEvalBranchQuota(15000); for (0..a_pins.len) |n_i| { // obtenemos el pin en función del indice const n_pin = get_pin4index(n_i + N_START); // obtenemos una nueva posición en el array const n_pos = get_permuted_index(n_i, N_TOTAL_PINS); // convertirmos el pin a cadena rellena con ceros por la izquierda a_pins[n_pos] = left_pad_zeros(n_pin, N_PIN_LENGTH); } } // imprimimos los primeros 5 y los últimos 5 // PIN para comprobar el resultado for (a_pins[0..5].*, 0..) |s_pin, n_i| { print("a_pins[{}]: {s}\n", .{ n_i, s_pin }); } print("...\n", .{}); const n_last = a_pins.len; for (a_pins[n_last - 5 .. n_last].*, n_last - 5..) |s_pin, n_i| { print("a_pins[{}]: {s}\n", .{ n_i, s_pin }); } } |
|
$ zig run pins_permuted.zig |
|
a_pins[0]: 015251 a_pins[1]: 012210 a_pins[2]: 015792 a_pins[3]: 028497 a_pins[4]: 000825 ... a_pins[995]: 047301 a_pins[996]: 022145 a_pins[997]: 097612 a_pins[998]: 027702 a_pins[999]: 066915 |
Como ves el orden de los PINs ha cambiado, aunque el contenido sea el mismo.
Hemos usado un principio sencillo para efectuar la permutación:
- Teniendo un índice I, si multiplicamos I por un número grande P y luego aplicamos % 1000 (el módulo de 1000), obtenemos un número muy grande y nos quedamos con sus tres últimas cifras.
- Si
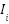 es un índice del array de los PINs, que tiene 1000 elementos (por eso hacemos %
1000) el resultado de esta operación sea cual sea
es un índice del array de los PINs, que tiene 1000 elementos (por eso hacemos %
1000) el resultado de esta operación sea cual sea 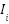 será un número en el rango de 0 a 999 (lógicamente el 0 no cambiará ya que 0*P %1000 = 0).
será un número en el rango de 0 a 999 (lógicamente el 0 no cambiará ya que 0*P %1000 = 0). - Cuanto más grande sea P, más grande será el resultado de la multiplicación. Imagina si el resultado es un número de 12 cifras o 20 cifras, esas tres últimas cifras que nos interesan, serán mucho más diversas en la secuencia que si como resultado tenemos un número de solo 4 cifras y vamos cogiendo ese 75% de su “capital” de dígitos.
- Nuestro objetivo es obtener el resultado de esta operación para cada índice:
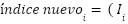
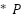 ) % N
) % N
En nuestro caso:
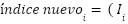
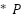 ) % 1000
) % 1000
Y de esta forma tan sencilla tenemos los índices permutados: los valores ya no están puestos en los mismos sitios. ¡Gran trabajo!
Ehem. Es sencillo… pero, no tan, tan sencillo. Hay que tener en cuenta una cosa más.
Si eliges un número grande cualquiera, por ejemplo 123456780 como P (sí mucha gente teclea así los números “al azar”, según van las teclas), vas a observar un fallo en este planteamiento: nuestro array será un desastre. El resultado empezará a repetirse causando colisiones (sobreescribir el mismo índice) y dejando huecos (posiciones sin asignar).
Nos falta un detalle clave.
Observemos el número N, en nuestro caso 1000:
1000 = 10³
10³ = 2³ * 5³
Y ahora observemos P = 123456780:
123456780 / 2 = 61728390
123456780 / 5 = 24691356
Nuestro número P comparte los factores con 1000: el 2 y el 5
Para asegurarnos de que esto no suceda necesitamos que el máximo común divisor de N y P sea 1.
- “¿Pero y eso existe?”
- Sí. Si pasa eso, en matemáticas se dice que N y P son coprimos.
- “¿Cómo encontrarlo?”
La forma más directa es usar unos números, que probablemente te sonarán y que en matemáticas se llaman números primos. Son aquellos números que son divisibles solo por 1 y por ellos mismos.
Por suerte estos números puedes cogerlos de una lista ya hecha. No hace falta que los calcules tú mismo. De hecho uno de los grandes retos matemáticos es precisamente buscar números primos muy, muy grandes - algo que sin la programación no hubiese sido posible.
Si usamos como P un número primo grande como por ejemplo 524287,- un número primo con cierta fama, prestigio y apellido Mersenne, heredado del gran matemático que lo estudió (y que te animo a buscar después), - obtenemos un valor que es divisible por 524287, por el número I y por 1. Pero lo importante es que no comparte factores con 1000.
Puedes comprobar que 524287 dividido entre 2 o 5 no da un número entero.
Por lo tanto, cuando tenemos un índice I cuyo valor está en el rango 0 a 999 y lo multiplicamos por 524287 y luego aplicamos % 1000 (siendo 524287 y 1000 coprimos) nos encontraremos con lo siguiente:
- El resultado caerá lógicamente entre 0 y 999 (nos quedamos las tres últimas cifras),
- Pero además, el resultado aunque caiga en ese rango, nunca será igual a su valor original I, salvo en el caso de que I = 0.
- Y lo más importante: todos los índices serán completados sin repetir ninguno.